Algorithms present in the toolbox

Shortest Path First algorithm

The toolbox contains a flexible implementation of the SPF algorithm and its constrained extension CSPF. The implementation is very efficient and uses a priority queue to store the list of temporary visited nodes. For computing the path of a LSP with a given reservation, the CSPF skips links that do not meet the bandwidth requirement. The scenario section explains in more detail how to use the CSPF to compute a LSP with the toolbox. Differents metrics can be used by the CSPF:

• IGP metric given in the topology (called CSPF)
• IGP TE metric given in the topology (called CSPFTEMetric)
• the inverse of the link capacity (called CSPFInvCap)
• the inverse of the reservable bandwidth (called CSPFInvFreeBw)
• 1 for each link (called CSPFHopCount)

Each different CSPF method has a name (between parentheses) used by the scenario to identify which metric to use.

Note that the implementation allows the efficient computation of all the paths from a particular source to all the destinations or from all the sources to a particular destination.

The CSPF implementation is also able to compute backup paths, both detour (one-to-one) and bypass (facility) LSPs. These calculated detour paths can be either local or global, link disjoint or node disjoint. CSPF has specific parameters for local backup computation. These are useless for global backup.

• mergePointLocation Can be "nearest" or "farthest". Indicates where the the local backup should merge with the primary path.
• mergePointPriority Can be "cost" or "location". Indicates if the path should be cost minimal among all possible merging point location or if the parameter mergePointLocation has the priority.
• stopOnError Can be true or false. If a local backup can't be computed, the other computed backups are returned if true, else an error condition occurs.

DAMOTE

We will first begin by introducing DAMOTE itself, and then see which additional parameters can be passed to corresponding scenario events to deal with the power of DAMOTE.

DAMOTE (Decentralized Agent for MPLS Online Traffic Engineering) provides two main basic functionalities:

• QoS-based routing of Diffserv LSPs (Label Switched Paths) under constraints.
• Local and global detour (backup) LSP routing for fast restoration

Let us review both of them.

The first main function of DAMOTE is to compute primary paths at ingress nodes, in a way similar to the classical CSPF (Constraint Shortest Path First). This means that all edge nodes will compute and set up the "best" path for any given LSP for which they are the ingress. This computation requires that ingress nodes have enough information about all link states in the network. This is usually achieved by using extensions of link-state routing protocols like OSPF-TE or ISIS-TE, which flood the network regularly with updated link-states.

Although similar in principle to CSPF, our scheme generalizes it in several ways. While CSPF is a simple SPF on a pruned topology, obtained by removing links that have not enough capacity to accept the new LSP, DAMOTE can perform much clever optimizations based on a network-wide score function. Examples of such functions are: load balancing, hybrid load balancing (where long detours are penalized), pre-emption-aware routing (where LSP reroutings are penalized). DAMOTE is generic in the sense that this score function is a parameter of the algorithm. Like in CSPF, constraints can be taken into account, but here again the constraints can be parameterised quite freely. Typical constraints refer to the available bandwidth on links per class type (CT), or to pre-emption levels. For example, it is possible to specify that an LSP of a given CT can only be accepted on a link if there is enough unreserved bandwidth for this CT by counting only the resources reserved by LSPs at higher pre-emption levels. This allows us to pre-empt other LSPs if needed. In that case, DAMOTE can also calculate the "best" subset of LSPs to pre-empt.

DAMOTE can also compute local detour LSPs for fast rerouting. In our approach, each primary can be protected by a series of detour LSPs, each of them originating at the node immediately upstream of any given link on the primary path. Those detour LSPs thus protect the downstream node (if possible) or the downstream link and merges with the primary LSP anywhere between the protected resource (exclusive) and the egress node (inclusive). Those many LSPs have to be pre-established for fast rerouting in case of failure, and provisioned with bandwidth resource. In terms of bandwidth consumption, this scheme is only viable if detour LSPs are allowed to share bandwidth among themselves or with primary LSPs, which is what we have achieved. The main idea is that we assume that at most one link or node will fail at the same time in the network. Under this assumption, we can share bandwidth between LSP that will never be activated together.

We will now explain which additional parameters can be passed to corresponding scenario events to deal with the power of DAMOTE.

Starting DAMOTE

DAMOTE can be started using the startAlgo scenario event (see 9.8.3). If backup LSPs need to be calculated and bandwidth sharing is a desirable feature, the domain must be loaded with bandwidth sharing enabled (see loadDomain scenario event 9.2.5).

By default, DAMOTE is configured with a hybrid score function (load balancing with traffic minimization contribution). But DAMOTE can also use pure load balancing score function, delay-oriented score function, min-hop routing,...  Let us review the available options.

Pure load balancing score function

DAMOTE can first be used with a pure load balancing score function, which is the following:

$$\sum_{(i,j) \in {\cal U}}\left(\frac{L_{(i,j)}}{\omega^{cap}(i,j)}- \overline{\frac{L}{\omega^{cap}}}\right)^2$$

$$with \quad \overline{\frac{L}{\omega^{cap}}}=\frac{1}{ \mid {\cal U} \mid }\sum_{(i,j) \in {\cal U}}\frac{L_{(i,j)}}{\omega^{cap}(i,j)}$$

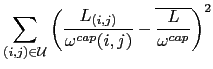
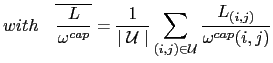
the mean of the relative link load throughout the network. This function is then the variance on the relative link load and, as such, represents the deviation from the optimal load balancing situation. In a perfectly balanced network, this deviation would be zero for all links so that all would be occupied in exactly the same proportions.

To use DAMOTE with a pure load balancing score function, you must set parameter ``loadBal'' to 1 and parameter ``tMin'' to 0 within the StartAlgo event.

Hybrid load balancing score function

The main problem with the load-balancing function presented above is that the only thing it tries to do is to flatten the relative load throughout the network. It will not matter if some of the paths go a long way around in order to achieve a better load-balancing. We must then try to limit the length of the paths chosen for the LSPs by adding a kind of "shortest path length" term to the objective function.

Our "traffic minimization" term is the sum of the square relative link loads,

$$\sum_{(i,j) \in {\cal U}}\left(\frac{L_{(i,j)}}{\omega^{cap}(i,j)}\right)^2$$

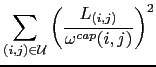
As a consequence, the compromise between load balancing and traffic minimization can be expressed as follows

$$loadBal*\sum_{(i,j) \in {\cal U}}\left(\frac{L_{(i,j)}}{\omega^{c... ...Min*\sum_{(i,j) \in {\cal U}}\left(\frac{L_{(i,j)}}{\omega^{cap}(i,j)}\right)^2$$

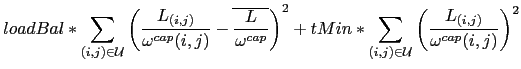
The (weighted) combination of both terms will give more importance to the load-balancing term if the deviation is high enough to justify the detour, else it will let the "shortest path" term minimize the resources used.

By default, DAMOTE is configured with ``loadBal'' equals to 2 and ``tMin'' equals to 1. You can change freely these two parameters.

Delay-oriented score function

Another available objective function is an average delay objective function

$$\sum_{(i,j) \in {\cal U}}\frac{1}{\omega^{cap}(i,j)-L_{(i,j)}}$$

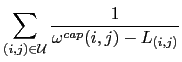
Since, for a packet size $P$ , $\frac{P}{\omega^{cap}(i,j)-L_{(i,j)}}$ approximates the queuing and transmission delay on link $(i,j)$ , optimizing this function will strive to minimize the average delay throughout the network. This will naturally lead to load-balance the network. Moreover, this objective has a built-in traffic minimization feature in the sense that long paths would degrade the average delay and are therefore discouraged.

To use this objective function, you must set ``loadBal'' to 0, ``tMin'' to 0 and ``delay'' to 1.

Shortest-path score function

Finally, if you want to use min-hop routing, you can set ``loadBal'' to 0, ``tMin'' to 0 and ``load'' to 1.

Computing a primary path with DAMOTE

An LSP can be computed with DAMOTE using the LSPCreation scenario event (see 9.3.11. When computing an LSP, you can pass an additional parameter to DAMOTE called preempt (boolean). This parameters tells DAMOTE whether it can preempt LSPs to establish the new one. In this case, DAMOTE returns a list of LSPs to preempt, and immediately deletes them from its own database. These LSPs are also removed from the toolbox database itself. Diffserv parameters can also be passed, but note that DAMOTE does not correctly support preemption when multiple categories of services (CTs) are used (to be fixed in the future). If you plan to use preemption, please only specify one category of service and several preemption levels for this category of service.

Additionnal note on preemption levels and categories of service

The default library (lib/libdamote.so) included in the release supports up to eight preemption levels and eight class types. If speed is a main concern for you and if you are using DAMOTE in a single class type and single preemption level environnement, you should link libdamote.so to libdamote11.so (instead of libdamote88.so) in order to increase speed perforcalculatemance.

Computing backups paths with DAMOTE

Detour LSPs can be created with the scenario event LSPBackupCreation. DAMOTE supports end-to-end and local detour. Corresponding parameters can then be passed to the scenario event.

Restrictions

Inside TOTEM, as bandwidth sharing is not compatible with Diffserv (see section 5.1), DAMOTE cannot be used to calculate backup paths when multiple priority levels are used.

Moreover, DAMOTE should be used to calculate backups only when bandwidth sharing is enabled. Otherwise, DAMOTE may return a backup path for which bandwidth is shared with other lsps; so it is possible that there is not enough free bandwidth to establish this lsp in TOTEM (as bandwidth sharing does not occur). In fact, an exception will be thrown if you try to compute a backup path without bandwidth sharing enabled.

MIRA

This section describes how to use the MIRA implementation included in the toolbox. This algorithm can be used to compute LSPs between two nodes of the network. In that sense, the use of this algorithm is quite similar to the use of CSPF algorithm.

Two MIRA algorithms are integrated in the TOTEM Toolbox : NEWMIRA (described in [6]) and Simple MIRA (SMIRA, described in [7]). These algorithms are both based on the principle of Minimum Interference Routing. When you start the algorithm, it is needed to specify which algorithm you want to use. In order to specify which algorithm you want to use, you have to add a param XML element whose name is ``version'' and the value is either ``NEWMIRA'' or ``SMIRA''. By default, SMIRA is used.

The MIRA algorithms make distinction between ``EDGE'' nodes and ``CORE'' nodes. ``EDGE'' nodes can be LSPs extremity while ``CORE'' nodes can only be intermediate nodes. If the node type is not set, the node is considered as ``EDGE''. Report to section 3.1.2 to see how to define the node type in the topology file.

A example of scenario using MIRA can be found in

examples/simpleDomain/Scenario/create_lsp_mira.xml.

SAMCRA

This section describes how to use the SAMCRA implementation included in the toolbox. This algorithm can be used to compute LSPs between two nodes of the network. Once again, the use of this algorithm is quite similar to the use of CSPF algorithm.

SAMCRA is an exact multi-constrained shortest path algorithm that was originally proposed in [8] and later extended in [9]. The implementation of SAMCRA included in the toolbox is the one described in [9].

To use SAMCRA, you have first to start the algorithm (called XAMCRA) precising the QoS constraints you desire and the version of the algorithm (till now only SAMCRA is included, but we plan to integrate other algorithm of the X-AMCRA familly). Once started, you can compute a path using this algorithm precising the QoS constraint for the desired path. If one QoS constraint that was desired is not provided, we assume $\infty$ for this constraint (i.e. no constraint) and if one constraint is provided for a parameter that was not desired, it is discarded.

When starting the algorithm, you can use the following boolean parameters : useDelay, useMetric and useTEMetric. The bandwidth constraint is allways used. When routing a LSP using LSPCreation element, you can use the following routing parameters : DelayConstraint, MetricConstraint and TEMetricConstraint to specify corresponding constraints. The bandwidth constraint is included in the addLSP element.

You can find an example of scenario file using SAMCRA in

examples/abilene/Scenario/XAMCRA-fullmesh.xml.

optDivideTM

This algorithm consists of dividing the traffic matrix into $N$ sub-matrices, called strata, and route each of these independently. We can use two different implementations of this method in routers. The method can also be used to compute a very precise approximation of the optimal value of a given objective function for comparison to heuristic Traffic Engineering algorithms. For this application, the algorithm is very efficient on large topologies compared to an LP formulation.

More information about this algorithm can be found in paper [10].

You can find an example of scenario file using optDivideTM in

examples/abilene/Scenario/optDivideTM.xml.

CBGP

C-BGP is a BGP routing solver. It aims at computing the interdomain routes selected by BGP routers in a domain. The route computation relies on an accurate model of the BGP decision process [11] as well as several sources of input data. The model of the decision process takes into account every decision rule present in the genuine BGP decision process as well as the iBGP hierarchy (route-reflectors). More information on how C-BGP works can be obtained from the C-BGP web site [12].

The input data required by C-BGP includes intradomain and interdomain information. First, the knowledge of the interdomain routes learned through BGP from the neighbor domains is required. This information can be obtained from MRT [13] dumps collected on the genuine BGP routers or it can be introduced manually. The route computation also relies on the knowledge of the intradomain structure. Indeed, the BGP decision process relies at some point on the IGP weight of the interdomain paths from ingress to egress routers to perform its route selection. This is often related to as the hot-potato routing rule. For this purpose, C-BGP also contains a model of the intradomain routing relying on shortest-path computation. The intradomain structure knowledge is obtained from the TOTEM XML topology. Finally, C-BGP needs to be told what must be computed through a simulation scenario. See Section 9 for more information on the scenario events that are currently available in the TOTEM toolbox.

The C-BGP algorithm is available in the toolbox through the CBGP class in the package be.ac.ucl.ingi.totem. C-BGP currently provides the following functionnalities within the TOTEM toolbox. First, when the C-BGP algorithm is started (see Section 9.8.3), it builds an internal representation of the domain being considered from the TOTEM XML topology which was previously loaded. This includes building a model of the domain's network based on the topology element. The intradomain model built by C-BGP currently only takes into account the nodes, links and IGP weights found in the nodes and igp. It does not model the multiple interfaces of one node. Nor does it model multiple links between a pair of nodes.

The internal representation of the domain also contains a model of BGP routing. This includes nodes that are modelled as BGP routers and the BGP sessions that are established between the BGP routers. This information is also obtained from the TOTEM XML topology, within the bgp element (see Section 3.1.5).

Then, C-BGP makes possible running the path computation and later extracting information on the path computation results. Running the path computation requires calling the int simRun() method. In order to extract the paths selected by C-BGP, the following methods are provided:

• Vector netNodeGetRT(String sNodeAddr, String sPrefix)
  This method returns the content of the routing table of the node identified by sNodeAddr. The sNodeAddr is a string that contains the IP address of the node. The sPrefix arguments permits retrieving only the routes that match the given prefix. The sPrefix contains a CIDR prefix in the form ``address / mask length''.
• Vector bgpRouterGetRib(String sRouterAddr, String sPrefix)
  This method returns the content of the BGP routing information base (RIB) of the BGP router identified by sRouterAddr. The sRouterAddr is a string that contains the IP address of the router. The sPrefix arguments permits retrieving only the routes that match the given prefix. The sPrefix contains a CIDR prefix in the form ``address / mask length''.
• Vector bgpRouterGetAdjRib(String sRouterAddr, String sNeighborAddr, String sPrefix, boolean bIn)
  This method returns the content of the BGP routing adjacent information bases (Adj-RIBs) of the BGP router identified by sRouterAddr. The sRouterAddr is a string that contains the IP address of the router. The sNeighborAddr argument specifies the IP address of the peer corresponding to the requested Adj-RIB. The sPrefix arguments permits retrieving only the routes that match the given prefix. The sPrefix contains a CIDR prefix in the form ``address / mask length''. The bIn argument controls which Adj-RIB is requested. If bIn is true, the input Adj-RIB is returned. Otherwise, the output Adj-RIB is returned.

In order to load interdomain routes in C-BGP, the Java class provides the following method: int bgpRouterLoadRib(String sRouterAddr, String sFileName). This method loads the content of the specified MRT dump file into the BGP router identified with the sRouterAddr argument. The MRT file must be provided uncompressed in ASCII format. Use the route_btoa conversion tool provided with the MRTd routing toolkit [13] for this purpose.

A convenient way to call C-BGP commands from the TOTEM toolbox is to rely on the int runCmd(String sCommand) method. The command takes a single argument, sCommand, which is a string containing a C-BGP command. If it is a valid C-BGP command, it is executed.

Many additional methods are provided, but not yet documented. Please refer to C-BGP's documentation [12] and C-BGP's Java classes for more details.

IGP-WO

IGP-WO (Interior Gateway Protocol-Weight Optimization) module aims at finding a link weight setting in the domain for an optimal load balancing. It provides a routing scheme adapted to the traffic demand matrix for congestion avoidance. The main inputs to the IGP-WO module are:

• Network topology: routers (nodes), links (arcs), link capacities
• Traffic demand matrix: source, destination, demand (bandwidth)
• Number of iterations: total number of iterations used in the heuristic search
• Maximum weight value ($W_{max}$ ): maximum weight value that can be assigned to links

The program yields an output as the weights for the links in the network. Here are some remarks regarding the current version of the tool.

• Multiple path routing: The traffic is assumed to be split equally among all of the shortest paths.

• A special objective function is used. Each link is assigned a function, which is convex and piecewise linearly increasing with the total load on the link. The main objective is to minimize the sum of these functions over all the links. For the definition of the function, see [14] or [15].

Since the problem of finding the optimal weight setting is NP-hard (no efficient algorithm available), a heuristic algorithm is applied to find a good but not necessarily optimal solution [15]. The algorithm is based on a well-known heuristic technique, called tabu search [16], whose attributes are summarized as follows:

• Solution representation: The solution is represented as a vector of weights. The weights are restricted to be integers in the range of $[1, W_{max}]$ .

• Neighborhood structure: Two types of neighborhood search are carried out.
  • Single weight change: The weight of a randomly selected link is changed.

  • Evenly balancing flows: Given a destination node ($t$ ), another node ($u$ ) is selected randomly among the ones that are on any shortest path toward $t$ . The weights of the arcs outgoing from $u$ is adjusted in such a way that the traffic from $u$ to $t$ is shared among multiple arcs. The weight change is restricted to the arcs which have less load than a threshold. The changes leading infeasible weight values are also avoided.
• Tabu lists: Tabu lists are used in tabu search to avoid cycling during the whole run. In order to save memory and time, special hash functions are utilized in IGP-WO.

• Diversification: Diversification is carried out when the working solution is not improved for $300$ iterations. During the diversification, each link weight is changed with a probability rate $10\%$ by adding a randomly chosen integer between $[-2, +2]$ . If the resulting weight is infeasible (less than $1$ or larger than $W_{max}$ ), it is forced to the corresponding bound value.

• Neighborhood Sampling: At each iteration, a proportion of the neighborhood is evaluated due to the large size of the problems. The initial rate by which the neighborhood is sampled is determined by the users. During the algorithm run, the value of the sampling rate is updated. If the current solution is improved, the sampling rate is divided by three, if not it is multiplied by two. The upper and lower bounds of the sampling rate are determined by the users, too.

The main IGP-WO algorithm is written in C and integrated through JNI. The IGPWO class is located in the package be.ac.ucl.poms.repository.IGPWO. The following method is provided by IGP-WO:

where ASID and TMID represent the domain and traffic matrix idenditification numbers. IGP-WO supports multiple traffic matrices. In case of multiple traffic matrices, the algorithm minimizes the sum of objective functions over the given traffic matrices.

num_iters ans w_max is the number of iterations and maximum possible weight value, respectively. random_initial determines whether the initial solution of the algorithm is created randomly, or is assigned to the currently used weights in the network. seed (default 0) is used for the random number generator. min_samp_rate, max_samp_rate, init_samp_rate control the sampling rate during the algorithm run. The sampling rate is not allowed not to go behind min_samp_rate and max_samp_rate.

The default value for the number of iterations is set to $150$ . The default value is kept low for the small example problems in the toolbox. If you have a large problem, it is suggested to assign a higher value to num_iters. The run time of the program increases with the number of iterations.

The default value for w_max is set to $50$ . The maximum value that can be given to w_max is $65535$ . The authors of the program suggest not to give a very large value for w_max. As the value increases, the output weights become less user-friendly and the running time increases due to the computations necessary for hash table values.

The default values for min_samp_rate, max_samp_rate, init_samp_rate are 0.01, 0.4 and 0.2, respectively. The running time of the algorithm increases with the sampling rate control parameters.

FastIPMetric

This module provides a fast and efficient metric generation for intra-domain routing. It is based on the Multi Commodity Network Flow Problem (MCNFP), which is a relaxation of IGP routing. We use an arc-based linear programming (LP) formulation of the Multi Commodity Network Flow problem to generate IGP weights. The objective is to minimize the piece-wise linear function $\Phi$ , which heavily penalizes over-utilized arcs as the their traffic load increase [14].

The mathematical model assumes the following parameters as given:

• a network that consists of nodes and arcs, $G=(N,A)$
• a traffic matrix, TM=( $\vert N\vert\times \vert N\vert$ )
• arc capacities, $c_{a}$ , $a \in A$

The decision variables are the following:

• load on arc $a \in A$ , $l_{a}$
• flow on arc $a \in A$ destined to $d \in N$ , $f_{a}^{d}$

The objective function is defined as $\Phi=\sum_{(a)\in A}\phi_{a}$ , where:

• $\phi_{a} \geq \alpha_{z}l_{a} - \beta_{z}c_{a}$ , $a \in A, z \in Z$
• $\alpha_{z}$ and $\beta_{z}$ are the coefficients and
• $Z$ is the set of break points of the objective function.

The model is coded in AMPL and the free GLPK package is used for solving the LP. GLPK is not included in the TOTEM distribution, therefore it should be installed seperately [17]. When $FastIPMetric$ is called in a scenario, the optimal solution of the MCNFP is calculated with respect to the inputs $G$ and TM. Then the dual vector of the costraints, $\Omega$ , which define link loads in the primal LP is retrieved. $\Omega$ , is the vector of the optimum arc price for the MCNFP. In $FastIPMetric$ , we use $\Omega$ as a link metric for IGP routing. For more details on this method, the user is referred to [18]. In the Scenario files, the algorithm should be used with the ECMP algorithm in order to be able to simulate $\Omega$ over $G$ and TM. A sample scenario (FastIPMetric.xml) is provided in /examples/abilene/Scenario/.

SAMTE

TOTEM also includes an hybrid IP/MPLS optimization method called SAMTE (Scalable Approach for MPLS Traffic Engineering). The idea of SAMTE is to combine both the simplicity and robustness of IGP routing and the flexibility of MPLS. This approach lies between the pure IP metric-based optimization (as IGP-WO) and the full mesh of LSPs. SAMTE uses the simulated annealing meta-heuristic to find a small number of LSPs (given as parameter) to establish in the network. The combination of the set of LSPs computed by SAMTE and the IGP routing for remaining flows optimise a given operational objective.

To use SAMTE, you first have to generate a Candidate Path List using the samte:generateCPL scenario element. This element accept the following parameters nbPath (the number of path to generater per source destination pair of nodes), maxDepth (the maximal number of nodes per path), verbose (print some information while generating the candidate path list) and fileName which specifies the file where to store the candidate path list. Once you have a candidate path list (be carefull, this list can take a huge amount of place on your hard disk !), you can use SAMTE with the scenario event samte:SAMTE. You have to provide the Candidate Path List file with the parameter cplName. You can also specify the number of runs of the algorithm (nbRun), the number of LSP to establish (nbLSP) and the Traffic Matrix to use ( TMID). The subelement samte:simulatedAnnealing configures the parameters of the simulated annealing heuristic via the parameters T0 the initial temperature, alpha the cooling factor, L the size of the plateau and E, $\epsilon$ , parameter for the stopping conditions. The subelement of samte:simulatedAnnealing is samte:objectiveFunction which specify the used objective function.

To show the link loads with the established LSPs, you have to use the ShowLinkInfo element with the type set to LOAD_BIS. This means Basic IGP Shortcut. This specifies the traffic that is routed on each LSP.

An example of use of SAMTE can be found in

examples/abilene/Scenario/samte.xml.

Multi Commodity Flow

This algorithm tries to solve the routing problem by using a linear programming formulation. It uses the free program "glpsol" to solve the routing problem. It tries to optimize the maximum link utilization. The model used is located in the file src/resources/modelAMPL/mcf-min-maxUtil.mod. You must have the "glpsol" executable in order to use this algorithm.

Reopt

This algorithm written by Sandford Bessler from FTW⁷ allows to dimension an LSP. It is written in AMPL and uses the CPLEX solver. It is based on a MCF problem and uses multiple explicit paths calculated in advance. The idea of this algorithm is to adapt existing LSPs to new traffic conditions while minimizing the number of LSP size changes.

You can find more information about this algorithm in [19].

LSPDimensioning

This algorithm written by Hung Tuan Tran from FTW is an adaptive provisioning algorithm based on:

1. Traffic load measurements
2. Packet-level target QoS constraint

   $$P(delay > D) < \epsilon$$ (3)

   
   
   where $D$ is the given delay bound and $\epsilon$ the given delay violation probability.

The traffic load is measured in a slot-by-slot manner. A certain number of such measurement slots constitutes a resizing window. The bandwidth is recalculated and updated (using one of the four prediction schemes) at the end of each resizing window and the newly assigned bandwidth is valid for the next resizing window. The algorithm is written in C and was integrated thanks to JNI.

More details about this algorithm can be found in [20].

ComputeMCNFOptimalRouting

This algorithm computes the optimal routing for an objective function given as an argument, using the ILOG CPLEX linear programming solver [21]. The available objective function are those cited in [22], i.e.

• the Fortz objective function. This function can also be optimized using the IGP-WO algorithm (see 8.7 subsection).
• the MIRA objective function, which minimizes the sum of the max-flows between each pair of nodes of the network.
• the Blanchy objective function, which takes an alpha parameter. The type of this parameter is double, and its defalut value is 1.0. This function is the compromise between load balancing and traffic minimization seen in subsection 8.2.
• the MeanDelay ( $\frac{1}{c_a-l_a}$ ) and WMeanDelay ( $\frac{l_a}{c_a-l_a}$ ) objective functions. In these cases, piecewise linear approximations of the functions are computed. The nbInt parameter can be set to define the number of intervals of this approximation. The defalut value for nbInt is 9.
• the InvCap ($\sum u_a$ ), MinHop ($\sum l_a$ ) and umax ($\max u_a$ ) objective functions.
• the Degrande objective function ( $C_B \cdot u_{max} + C_U \cdot \sum u_a$ ), which takes two parameters : C_B and C_U. Both of these parameters are of type double and their default values are both 1.0.

The optimization is executed for the default domain, using the traffic matrix given in the scenario file. For each objective function, two formulations of the problem can be used :

1. the Node-Link formulation.
2. the Link-Path formulation. This formulation uses the computeAllDistinctRoute method to compute the paths between each pair of nodes. The user has to set the nbPaths argument, which defines the maximum number of paths to be computed for each pair.

An example of scenario using this algorithm can be found in
/examples/abilene/Scenario/cplexMCNF.xml

Since the CPLEX optimizer is not free, the default compiling options don't build this class. People who own the CPLEX licence (and thus have the cplex.jar file) can compile it as explained below :

• First add the path to cplex.jar in the MANIFEST.MF file which can be found in the src/java/be/ac/ulg/montefiore/run/totem/repository/cplexMCNF/
  META-INF/ directory :

  Class-Path: ../../dist/totem-3.0.jar *PATH_TO_CPLEX*/cplex.jar
  

• Add a reference to the XML schema in the preferences.xml file located in the src/resources directory (or in the preferences.xml file under the totem root folder if present). Under the SCENARIO-SCHEMA-LOCATION key, add the string

  http://jaxb.model.scenario.cplexMCNF.repository.totem.run.montefiore.ulg.ac.be
  http://totem.run.montefiore.ulg.ac.be/Schema/CPLEX-MCNF-Scenario-v1_0.xsd
  

  and under the SCENARIO-PACKAGES key, add the string

  be.ac.ulg.montefiore.run.totem.repository.cplexMCNF.scenario.model.jaxb
  

  separated by a ":" character.

  An example of preferences file that has CPLEX enabled is located in /src/resources/cplexMCNF/. Alternatively you can replace your existing preferences file with this one.

• Build the toolbox using the following command :

  ant clean build
  

• Then build the plugin :

  	ant -Dplugin=be/ac/ulg/montefiore/run/totem/repository/cplexMCNF/
      -Dplugin.lib=*PATH_TO_CPLEX*/cplex.jar
      build-given-plugin
  

  You can ommit the -Dplugin.lib line if the cplex.jar is located in the totem library directory (totem/lib/java).